中国大学MOOC-陈越、何钦铭-数据结构
1.树的同构
定两棵树T1和T2。如果T1可以通过若干次左右孩子互换就变成T2,则我们称两棵树是“同构”的。例如图1给出的两棵树就是同构的,因为我们把其中一棵树的结点A、B、G的左右孩子互换后,就得到另外一棵树。而图2就不是同构的。
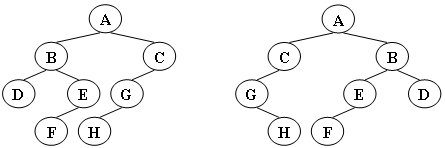
图1
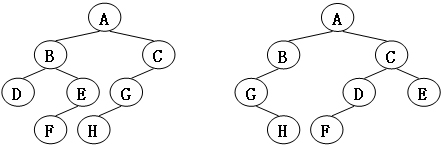
图2
现给定两棵树,请你判断它们是否是同构的。
输入格式:
输入给出2棵二叉树树的信息。对于每棵树,首先在一行中给出一个非负整数NN (\le 10≤10),即该树的结点数(此时假设结点从0到N-1N−1编号);随后NN行,第ii行对应编号第ii个结点,给出该结点中存储的1个英文大写字母、其左孩子结点的编号、右孩子结点的编号。如果孩子结点为空,则在相应位置上给出“-”。给出的数据间用一个空格分隔。注意:题目保证每个结点中存储的字母是不同的。
输出格式:
如果两棵树是同构的,输出“Yes”,否则输出“No”。
输入样例1(对应图1):
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 |
8 A 1 2 B 3 4 C 5 - D - - E 6 - G 7 - F - - H - - 8 G - 4 B 7 6 F - - A 5 1 H - - C 0 - D - - E 2 - |
输出样例1:
|
1 |
Yes |
输入样例2(对应图2):
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 |
8 B 5 7 F - - A 0 3 C 6 - H - - D - - G 4 - E 1 - 8 D 6 - B 5 - E - - H - - C 0 2 G - 3 F - - A 1 4 |
输出样例2:
|
1 |
No |
程序代码:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 |
#include <stdio.h> #define MaxTree 10 #define ElementType char #define Tree int #define Null -1 struct TreeNode { ElementType Element; Tree Left; Tree Right; }T1[MaxTree],T2[MaxTree]; Tree BuildTree(struct TreeNode T[]) { int N,i,check[MaxTree]; Tree Root=Null; char cl,cr; scanf("%d\n",&N); if(N) { for(i=0;i<N;i++) check[i]=0; for(i=0;i<N;i++) { scanf("%c %c %c\n",&T[i].Element,&cl,&cr); if(cl!='-') { T[i].Left=cl-'0'; check[T[i].Left]=1; } else T[i].Left=Null; if(cr!='-') { T[i].Right=cr-'0'; check[T[i].Right]=1; } else T[i].Right=Null; } for(i=0;i<N;i++) if(!check[i]) break; Root=i; } return Root; } int Issame(Tree R1,Tree R2) { if((R1==Null)&&(R2==Null)) return 1; if(((R1==Null)&&(R2!=Null))||((R1!=Null)&&(R2==Null))) return 0; if(T1[R1].Element!=T2[R2].Element) return 0; if((T1[R1].Left==Null)&&(T2[R2].Left==Null)) return Issame(T1[R1].Right,T2[R2].Right); if(((T1[R1].Left!=Null)&&(T2[R2].Left!=Null))&&((T1[T1[R1].Left].Element)==(T2[T2[R2].Left].Element))) return (Issame(T1[R1].Left,T2[R2].Left)&&Issame(T1[R1].Right,T2[R2].Right)); else return (Issame(T1[R1].Left,T2[R2].Right)&&Issame(T1[R1].Right,T2[R2].Left)); } int main() { Tree R1,R2; R1=BuildTree(T1); R2=BuildTree(T2); if(Issame(R1,R2)) printf("Yes\n"); else printf("No\n"); return 0; } |
2.List Leaves
Given a tree, you are supposed to list all the leaves in the order of top down, and left to right.
Input Specification:
Each input file contains one test case. For each case, the first line gives a positive integer NN (\le 10≤10) which is the total number of nodes in the tree — and hence the nodes are numbered from 0 to N-1N−1. Then NN lines follow, each corresponds to a node, and gives the indices of the left and right children of the node. If the child does not exist, a “-” will be put at the position. Any pair of children are separated by a space.
Output Specification:
For each test case, print in one line all the leaves’ indices in the order of top down, and left to right. There must be exactly one space between any adjacent numbers, and no extra space at the end of the line.
Sample Input:
|
1 2 3 4 5 6 7 8 9 10 |
8 1 - - - 0 - 2 7 - - - - 5 - 4 6 |
Sample Output:
|
1 |
4 1 5 |
程序代码:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 |
#include <iostream> #include <queue> using namespace std; #define MaxTree 10 #define ElementType int #define Tree int #define Null -1 struct TreeNode { ElementType Element; Tree Left; Tree Right; }T[MaxTree]; Tree BuildTree(struct TreeNode T[]) { int N; bool check[MaxTree]; Tree Root=Null; char cl,cr; cin>>N; if(N) { for(int i=0;i<N;i++) check[i]=false; for(int i=0;i<N;i++) { T[i].Element=i; cin>>cl>>cr; if(cl!='-') { T[i].Left=cl-'0'; check[T[i].Left]=true; } else T[i].Left=Null; if(cr!='-') { T[i].Right=cr-'0'; check[T[i].Right]=true; } else T[i].Right=Null; } for(int i=0;i<N;i++) { if(!check[i]) { Root=i; break; } } } return Root; } int main() { queue<int> q; int res[MaxTree]; Tree R; R=BuildTree(T); if(R==Null) return 0; q.push(R); int i=0; while(!q.empty()) { R=q.front(); q.pop(); if((T[R].Left==Null)&&(T[R].Right==Null)) { res[i]=T[R].Element; i++; } if(T[R].Left!=Null) q.push(T[R].Left); if(T[R].Right!=Null) q.push(T[R].Right); } for(int j=0;j<i-1;j++) cout<<res[j]<<' '; cout<<res[i-1]<<endl; return 0; } |